1.
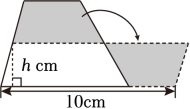
我国古代数学家刘徽利用“出入相补”原理计算梯形面积。如图,转化后的平行四边形的底是10cm , 高是hcm , 原梯形的高是 cm , 面积是 cm2。
【考点】
平行四边形的面积;
平行四边形的切拼;
基础巩固
能力提升
变式训练
拓展培优