如图，已知△ACB和△ECD都是等腰直角三角形，CA＝CB，CE=CD，△ACB的顶点A在△ECD的斜边ED上，连接BD．

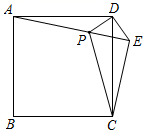
1. 如图，已知△ACB和△ECD都是等腰直角三角形，CA＝CB，CE=CD，△ACB的顶点A在△ECD的斜边ED上，连接BD．

(1) 求证：BD＝AE；

(2) 求证：AE²+AD²＝2AC² ．

【考点】

勾股定理; 等腰直角三角形; 三角形全等的判定-SAS;

【答案】

您现在未登录，无法查看试题答案与解析。登录

解答题普通

1. 已知，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 为 $\text{[math]}$ 边上一点， $\text{[math]}$ 为射线 $\text{[math]}$ 上一点，连接 $\text{[math]}$ 、 $\text{[math]}$ ．

(1) 如图1，若 $\text{[math]}$ ， $\text{[math]}$ 平分 $\text{[math]}$ ，求 $\text{[math]}$ 的度数；

(2) 如图2，若 $\text{[math]}$ ，求 $\text{[math]}$ 的度数；

(3) 如图3，若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 在 $\text{[math]}$ ， $\text{[math]}$ 之间，且 $\text{[math]}$ ，求 $\text{[math]}$ 的长．

解答题困难

2. 在直角 $\text{[math]}$ 中， $\text{[math]}$ 为斜边 $\text{[math]}$ 的中点， $\text{[math]}$ 、 $\text{[math]}$ 分别在 $\text{[math]}$ 、 $\text{[math]}$ 上， $\text{[math]}$ ，已知 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ ．

解答题普通

3. 等腰 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ．

(1) 如图1， $\text{[math]}$ ， $\text{[math]}$ 是等腰 $\text{[math]}$ 斜边 $\text{[math]}$ 上两动点，且 $\text{[math]}$ ，将△ABE绕点 $\text{[math]}$ 逆时针旋转 $\text{[math]}$ 后，得到△AFC ，连接 $\text{[math]}$ ．

①求证：△AED≌AFD．

②当 $\text{[math]}$ ， $\text{[math]}$ 时，求 $\text{[math]}$ 的长；

(2) 如图2，点 $\text{[math]}$ 是等腰 $\text{[math]}$ 斜边 $\text{[math]}$ 所在直线上的一动点，连接 $\text{[math]}$ ，以点 $\text{[math]}$ 为直角顶点作等腰Rt△ADE ，当 $\text{[math]}$ ， $\text{[math]}$ 时，则 $\text{[math]}$ 的长．（直接给出答案）．

解答题困难