1.
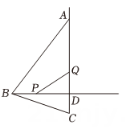
如图,在等腰△ABC中,AB=AC , BD⊥AC于点D , 已知BD=6,AD=8.

(1)
求CD的长.
(2)
动点P从点B出发,沿射线BD以每秒1个单位长度的速度运动,Q为射线DA上一点,DQ=BP , 连结PQ , 设点P运动的时间为t秒.
①当点P在线段BD上时,若△CPQ是以CP为腰的等腰三角形,求t的值.
②在点P的整个运动过程中,作点Q关于AP的对称点 , 连结
, 当
//AC时,请直接写出此时PD的长: ▲ .
【考点】
直角三角形全等的判定-HL;
勾股定理;
矩形的判定与性质;
等腰直角三角形;
三角形-动点问题;


