1.
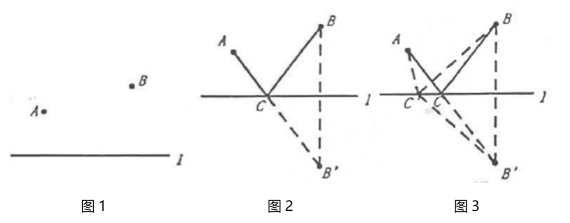
提出问题:早在古罗马时代,传说亚历山大城有一位精通数学和物理的学者——海伦.一天,一位将军专程拜访他,请教一个百思不得其解的问题:如图1,将军每天从军营出发,先到河边饮马,然后再去军营
开会,怎样走才能使路程最短?据说海伦略加思索就解决了它.这个问题被称为“将军饮马”的问题.你知道海伦是怎样解决这个问题的吗?
(1)
研究方法:第一步作其中一定点的对称点,第二步连接对称点和另一定点,第三步找与河(对称轴)的交点.如图2,此时 最短,由轴对称的性质可得
最短,由轴对称的性质可得 , 所以
, 所以 最短.如图3,在直线上任取点
最短.如图3,在直线上任取点 ,
,  的理由是:.
(2)
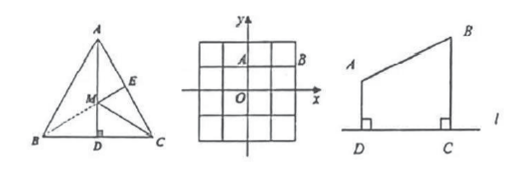
如图4,在等边
的理由是:.
(2)
如图4,在等边 ,
,  ,
,  ,
,  是
是 的中点,
的中点, 是
是 上的一点,则
上的一点,则 的最小值是;(请直接写出答案)
(3)
如图5,在平面直角坐标系中,已知点
的最小值是;(请直接写出答案)
(3)
如图5,在平面直角坐标系中,已知点 , 点
, 点 , 点
, 点 在
在 轴上运动,当
轴上运动,当 的值最小时,点
的值最小时,点 的坐标是;(请直接写出答案)
(4)
如图6,
的坐标是;(请直接写出答案)
(4)
如图6, 于点
于点 ,
,  于点
于点 , 且
, 且 ,
,  , 当点
, 当点 在直线
在直线 上运动时,
上运动时, 的最小值是.(请直接写出答案)
的最小值是.(请直接写出答案)
【考点】
两点之间线段最短;
等边三角形的性质;
轴对称的应用-最短距离问题;
能力提升


