1.
定义:若圆内接三角形是等腰三角形,我们就称这样的三角形为“圆等三角形”.

(1)
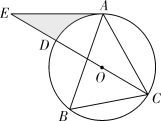
如图1,AB是⊙O的一条弦(非直径),若⊙O在上找一点C,使得△ABC是“圆等三角形”,则这样的点C能找到个.
(2)
如图2,四边形ABCD是⊙O的内接四边形,连结对角线BD,△ABD和△BCD均为“圆等三角形”,且AB=AD.
①当∠A=140°时,求∠ADC的度数;
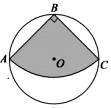
②如图3,当∠A=120°,AB=6时,求阴影部分的面积.
【考点】
等腰三角形的性质;
圆周角定理;
扇形面积的计算;