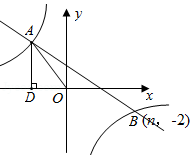
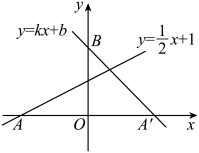
已知一次函数的图象经过，．

1. 已知一次函数的图象经过 $\text{[math]}$ ， $\text{[math]}$ ．

(1) 求一次函数解析式；

(2) 若正比例函数 $\text{[math]}$ 与线段 $\text{[math]}$ 有公共点，直接写出 $\text{[math]}$ 的取值范围．

【考点】

待定系数法求一次函数解析式; 两一次函数图象相交或平行问题;

【答案】

您现在未登录，无法查看试题答案与解析。登录

解答题困难

1. 如图直线： $\text{[math]}$ 经过点 $\text{[math]}$ ， $\text{[math]}$ ．

(1) 求直线 $\text{[math]}$ 的表达式；

(2) 若直线 $\text{[math]}$ 与直线 $\text{[math]}$ 相交于点 $\text{[math]}$ ，求点 $\text{[math]}$ 的坐标；

(3) 根据图象，直接写出关于 $\text{[math]}$ 的不等式 $\text{[math]}$ 的解集．

解答题普通

2. 在平面直角坐标系 $\text{[math]}$ 中，函数 $\text{[math]}$ 的图象经过点 $\text{[math]}$ 和 $\text{[math]}$ ，与过点 $\text{[math]}$ 且平行于 $\text{[math]}$ 轴的直线交于点 $\text{[math]}$ ．

(1) 求该函数的解析式及点 $\text{[math]}$ 的坐标；

(2) 当 $\text{[math]}$ 时，对于 $\text{[math]}$ 的每一个值，函数 $\text{[math]}$ 的值大于函数 $\text{[math]}$ 的值且小于 $\text{[math]}$ ，直接写出 $\text{[math]}$ 的值．

解答题普通

3. 如图，直线 $\text{[math]}$ 与x轴，y轴分别相交于 $\text{[math]}$ ， B两点．

(1) b的值是，点B的坐标为；

(2) 过B点的直线 $\text{[math]}$ 交x轴于点C ，且 $\text{[math]}$ ，求直线BC对应的函数表达式．

解答题普通