1.
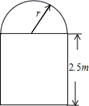
如图所示,用一段长为30 m的篱笆围成一个一边靠墙(墙的长度不限)的矩形菜园ABCD,设AB边的长为 .求:
.求:

(1)
菜园的面积 关于
关于 的函数表达式.
(2)
自变量
的函数表达式.
(2)
自变量 的取值范围.
的取值范围.
【考点】
列二次函数关系式;