1.
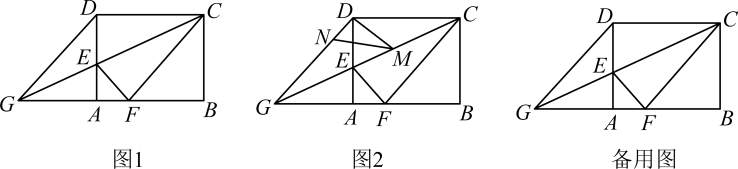
某数学活动小组在学完特殊的平行四边形之后,针对矩形中的折叠问题进行了研究.
如图 , 在矩形
, 在矩形 中,
中, ,
,  , 点
, 点 为
为 边上一点,将矩形
边上一点,将矩形 沿
沿 折叠,点
折叠,点 为点
为点 折叠后的对应点,过点
折叠后的对应点,过点 作
作 , 交折痕
, 交折痕 于点
于点 , 连接
, 连接 .
.

如图

(1)
猜想四边形 的形状,并证明你的结论;
的形状,并证明你的结论;
(2)
如图 , 连接
, 连接 , 当点
, 当点 落在
落在 上时,
上时, 的长为
的长为  用含
用含 的代数式表示
的代数式表示 ;
;
(3)
如图 , 当点
, 当点 落在
落在 上时,若
上时,若 , 请直接写出
, 请直接写出 的长.
的长.
【考点】
勾股定理;
菱形的判定与性质;
矩形的性质;
翻折变换(折叠问题);