1.
在直角坐标系中,已知点 ,
,  ,
,  , a是
, a是 的立方根,方程
的立方根,方程 是关于x,y的二元一次方程,d为不等式组
是关于x,y的二元一次方程,d为不等式组 的最大整数解.
的最大整数解.
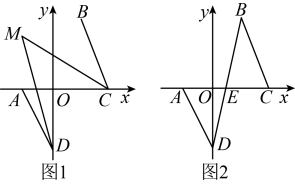
(1)
求点A、B、C的坐标;
(2)
如图1,若D为y轴负半轴上的一个动点,当 时,
时, 与
与 的平分线交于M点,求
的平分线交于M点,求 的度数;
(3)
如图2,若D为y轴负半轴上的一个动点,连BD交x轴于点E,问是否存在点D,使
的度数;
(3)
如图2,若D为y轴负半轴上的一个动点,连BD交x轴于点E,问是否存在点D,使 ?若存在,请求出D的纵坐标
?若存在,请求出D的纵坐标 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
【考点】
二元一次方程的概念;
解一元一次不等式组;
平行线的判定与性质;
列一元一次不等式组;
能力提升
