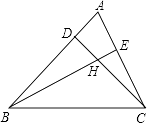
1.
在 中,
中, , 点
, 点 是直线
是直线 上一点
上一点 不与
不与 、
、 重合
重合 , 以
, 以 为一边在
为一边在 的右侧作
的右侧作 , 使
, 使 ,
,  , 连接
, 连接 E .
E .
(1)
如图1,当点 在线段
在线段 上,如果
上,如果 .
(2)
如图2,如果
.
(2)
如图2,如果 , 当点
, 当点 在线段
在线段 上移动,则
上移动,则 的度数是
的度数是 ;
(3)
如图2,当点
;
(3)
如图2,当点 在线段
在线段 上,如果
上,如果 ,
,  点为
点为 中
中 边上的一个动点
边上的一个动点 与
与 、
、 均不重合
均不重合 , 当点
, 当点 运动到什么位置时,
运动到什么位置时, 的周长最小?
的周长最小?

①则与
全等吗?请说明理由;
②求的度数;

【考点】
垂线段最短及其应用;
三角形内角和定理;
三角形全等及其性质;
三角形全等的判定;
等腰三角形的性质;