1.
如图,在 中,
中, ,
,  平分
平分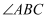 , 交
, 交 于点
于点 , 点
, 点 是
是 边上的点,以
边上的点,以 为弦的
为弦的 交
交 于点
于点 .
.


(1)
求证: 是
是 的切线;
(2)
若
的切线;
(2)
若 ,
,  , 求阴影部分的面积.
, 求阴影部分的面积.
【考点】
含30°角的直角三角形;
勾股定理;
垂径定理;
切线的判定;
扇形面积的计算;


