如图，在▱ABCD中，线段AC的垂直平分线交AC于O ，分别交BC ， AD于E ， F ，连接AE ， CF ．

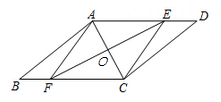
1. 如图，在▱ABCD中，线段AC的垂直平分线交AC于O ，分别交BC ， AD于E ， F ，连接AE ， CF ．

(1) 证明：四边形AECF是菱形；

(2) 在（1）的条件下，如果AC⊥AB ， ∠B＝30°，AE＝3，求四边形AECF的面积．

【考点】

平行四边形的判定与性质; 菱形的判定与性质;

【答案】

您现在未登录，无法查看试题答案与解析。登录

解答题普通

1. 如图，在菱形 $\text{[math]}$ 中， $\text{[math]}$ 是对角线，点 $\text{[math]}$ 是线段 $\text{[math]}$ 延长线上的一点，在线段 $\text{[math]}$ 的延长线上截取 $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 试判断四边形 $\text{[math]}$ 的形状，并说明理由．

解答题普通

2. 如图，在平行四边形ABCD中，点E，F，G，H分别在边AB，BC，CD，DA上，AE=CG，AH=CF.

(1) 如图（1）求证：四边形EFGH是平行四边形；

(2) 如图(2)若EG平分∠HEF，在不添加辅助线的条件下，直接写出长度等于EH的线段(不包括EH)

解答题普通

3. 在Rt△ABC中，∠BAC=90°，D是BC的中点，E是AD的中点，过点A作AF∥BC交BE的延长线于点F．

(1) 证明四边形ADCF是菱形；

(2) 若AC＝4，AB＝5，求菱形ADCF的面积．

解答题普通