1.
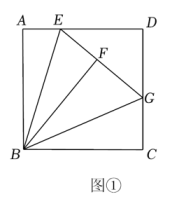
如图1,在矩形 中,
中, , 分别以
, 分别以 为边向外作正方形
为边向外作正方形 和正方形
和正方形 , 连接
, 连接 交
交 于点N,连接
于点N,连接 交
交 于点M.
于点M.

(1)
求证: ;
(2)
连接
;
(2)
连接  , 求
, 求 的长;
(3)
如图2,将正方形
的长;
(3)
如图2,将正方形 绕C点旋转,当F落在边
绕C点旋转,当F落在边 上时(点D旋转到
上时(点D旋转到 ),请直接写出
),请直接写出 的长为.
的长为.
【考点】
正方形的性质;
四边形的综合;
能力提升
真题演练