1.
(1)
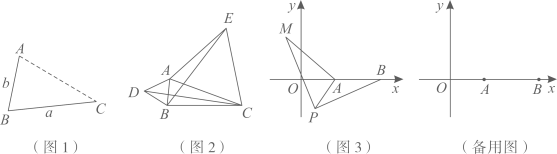
发现:如图 , 点
, 点 为线段
为线段 外一动点,且
外一动点,且 ,
,  .
(2)
应用:点
.
(2)
应用:点 为线段
为线段 外一动点,且
外一动点,且 ,
,  , 如图
, 如图 所示,分别以
所示,分别以 ,
,  为边,作等边三角形
为边,作等边三角形 和等边三角形
和等边三角形 , 连接
, 连接 ,
,  .
(3)
拓展:如图
.
(3)
拓展:如图 , 在平面直角坐标系中,点
, 在平面直角坐标系中,点 的坐标为
的坐标为 , 点
, 点 的坐标为
的坐标为 , 点
, 点 为线段
为线段 外一动点,且
外一动点,且 ,
,  ,
,  , 请直接写出线段
, 请直接写出线段 长的最大值及此时点
长的最大值及此时点 的坐标.
的坐标.
填空:当点位于时,线段
的长取得最大值,且最大值为
用含
,
的式子表示
①请找出图中与相等的线段,并说明理由;
②直接写出线段长的最大值.
【考点】
点的坐标;
等边三角形的性质;
旋转的性质;
等腰直角三角形;
三角形全等的判定-SAS;
能力提升
