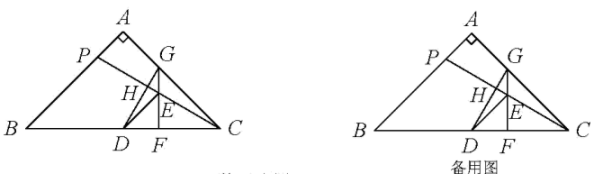1.
如图

(1)
问题发现:两个顶角相等的等腰三角形,如果具有公共的顶角的顶点,并把它们的底角顶点连接起来,则形成一组全等的三角形,我们把具有这种规律的图形称为“手拉手”图形,
(2)
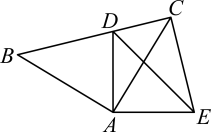
类比探究:如图2, 和ΔADE都是等腰三角形,即
和ΔADE都是等腰三角形,即 ,
,  , 且
, 且
 , B,C,D在同一条直线上.请判断线段
, B,C,D在同一条直线上.请判断线段 与
与 存在怎样的数量关系及位置关系,并说明理由.
(3)
问题解决:如图3,若ΔACB和ΔDCE均为等腰直角三角形,且CA=CB,CD=CE,∠ACB=∠DCE=90°,点A,D,E在同一条直线上,CM为ΔDCE中DE边上的高,连接BE,若AE=7,BE=2,请直接写出CM的长,不说明理由.
存在怎样的数量关系及位置关系,并说明理由.
(3)
问题解决:如图3,若ΔACB和ΔDCE均为等腰直角三角形,且CA=CB,CD=CE,∠ACB=∠DCE=90°,点A,D,E在同一条直线上,CM为ΔDCE中DE边上的高,连接BE,若AE=7,BE=2,请直接写出CM的长,不说明理由.
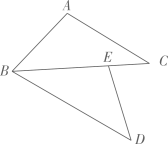
如图1,和ΔADE是顶角相等的等腰三角形,即
,
, 且
, 分别连接
,
. 求证:
;
【考点】
等腰直角三角形;
三角形全等的判定-SAS;
能力提升
真题演练