1.
几何模型在解题中有着重要作用,例如美味的“猪蹄模型”.
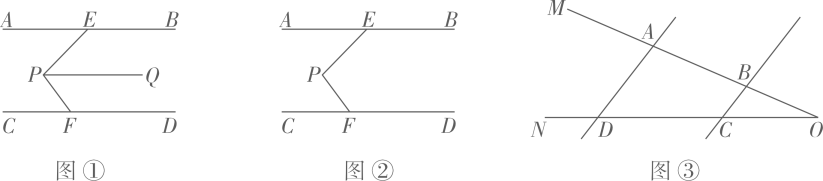
(1)
导入:如图①,已知 , 如果
, 如果 ,
,  , 则
, 则
 ;
(2)
发现:如图②,直线
;
(2)
发现:如图②,直线 , 请判断
, 请判断 与
与 之间的数量关系,并说明理由;
(3)
运用:如图③,已知
之间的数量关系,并说明理由;
(3)
运用:如图③,已知 在射线
在射线 上运动(点
上运动(点 与点
与点 三点不重合),
三点不重合), , 请用含
, 请用含 的代数式表示
的代数式表示 , 并说明理由.
, 并说明理由.
【考点】
平行线的性质;
平行线的判定与性质;
能力提升


