1.
阅读与思考:下面是一位同学的数学学习笔记,请仔细阅读并完成相应任务.
|
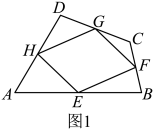
瓦里尼翁平行四边形 我们知道,如图1,在四边形
我查阅了许多资料,得知这个平行四边形
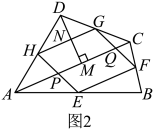
①当原四边形的对角线满足一定关系时,瓦里尼翁平行四边形可能是菱形、矩形或正方形. ②瓦里尼翁平行四边形的周长与原四边形对角线的长度也有一定关系. ③瓦里尼翁平行四边形的面积等于原四边形面积的一半.此结论可借助图1证明如下: 证明:如图2,连接 ∵
∴ ∵四边形 ∵ ∴四边形 ∵ |
任务:
(1)
填空:材料中的依据1是指:.
(2)
请用刻度尺、三角板等工具,画一个四边形 及它的瓦里尼翁平行四边形
及它的瓦里尼翁平行四边形 , 使得四边形
, 使得四边形 为矩形;(要求同时画出四边形
为矩形;(要求同时画出四边形 的对角线)
(3)
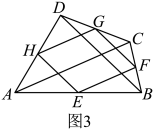
在图1中,分别连接
的对角线)
(3)
在图1中,分别连接 得到图3,请猜想瓦里尼翁平行四边形
得到图3,请猜想瓦里尼翁平行四边形 的周长与对角线
的周长与对角线 长度的关系,并证明你的结论.
长度的关系,并证明你的结论.
依据2是指:.
【考点】
平行四边形的判定与性质;
矩形的判定;
三角形的中位线定理;
中点四边形模型;