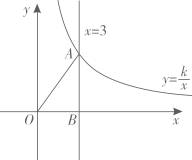
如图，在平面直角坐标系中，直线与双曲线相交于点A ，与x轴交于点B ，连接，．

1. 如图，在平面直角坐标系中，直线 $\text{[math]}$ 与双曲线 $\text{[math]}$ 相交于点A ，与x轴交于点B ，连接 $\text{[math]}$ ， $\text{[math]}$ ．

(1) 求双曲线 $\text{[math]}$ 的解析式；

(2) 若点C在双曲线上，且 $\text{[math]}$ ，求点C的坐标．

【考点】

待定系数法求反比例函数解析式; 相似三角形的判定与性质;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 如图，在锐角三角形ABC中，点D，E分别在边AC，AB上，AG⊥BC于点G，AF⊥DE于点F，∠EAF=∠GAC．

(1) 求证：△ADE∽△ABC；

(2) 若AD=3，AB=5，求 $\text{[math]}$ 的值．

综合题普通

2. 设函数 $\text{[math]}$ ，函数 $\text{[math]}$ （ $\text{[math]}$ ， $\text{[math]}$ ， b是常数， $\text{[math]}$ ， $\text{[math]}$ ）．若函数 $\text{[math]}$ 和函数 $\text{[math]}$ 的图象交于点 $\text{[math]}$ ，点 $\text{[math]}$ ．

(1) 求点 $\text{[math]}$ ， $\text{[math]}$ 的坐标．

(2) 求函数 $\text{[math]}$ ， $\text{[math]}$ 的表达式．

(3) 当 $\text{[math]}$ 时，直接写出 $\text{[math]}$ 的取值范围．

综合题普通

3. 若一个三角形一条边的平方等于另两条边的乘积，我们把这个三角形叫做比例三角形．

(1) 已知△ABC是比例三角形，AB=2，BC=3．请直接写出所有满足条件的AC的长；

(2) 如图1，在四边形ABCD中，AD∥BC，对角线BD平分∠ABC， ∠BAC=∠ADC．求证：△ABC是比例三角形；

(3) 如图2，在（2）的条件下，当∠ADC=90°时，求 $\text{[math]}$ 的值。

综合题困难