1.
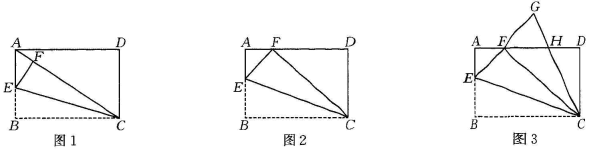
如图,在矩形 中,
中, , E是
, E是 上的一个动点.
上的一个动点.

(1)
如图1,连接 , G是对角线
, G是对角线 的三等分点,且
的三等分点,且 , 连
, 连 .当
.当 时,求
时,求 的长;
(2)
如图2,连接
的长;
(2)
如图2,连接 , 过点E作
, 过点E作 交线段
交线段 于点F,连接
于点F,连接 , 与
, 与 交于点P.当
交于点P.当 平分
平分 时,求
时,求 的长;
(3)
如图3,连接
的长;
(3)
如图3,连接 , 点H在
, 点H在 上,将
上,将 沿直线
沿直线 折叠,折叠后点D落在
折叠,折叠后点D落在 上的点
上的点 处,过点
处,过点 作
作 于点N,与
于点N,与 交于点M,且
交于点M,且 .求
.求 的面积.
的面积.
【考点】
翻折变换(折叠问题);
两条直线被一组平行线所截,所得的对应线段成比例;
相似三角形的判定与性质;
锐角三角函数的定义;
三角形全等的判定-ASA;
能力提升