1.
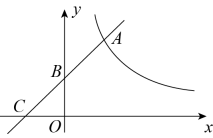
如图,直线 与反比例函数
与反比例函数 的图象交于点
的图象交于点 , 与
, 与 轴,
轴, 轴依次交于点B,点C.
轴依次交于点B,点C.
(1)
当 时,求
时,求 的值;
(2)
判定
的值;
(2)
判定 与
与 的比值能否与
的比值能否与 相等?若有,求线段
相等?若有,求线段 的长度;若没有,请说明理由.
的长度;若没有,请说明理由.
【考点】
一次函数的图象;
待定系数法求反比例函数解析式;
相似三角形的判定与性质;
反比例函数图象上点的坐标特征;
三角形全等的判定-AAS;