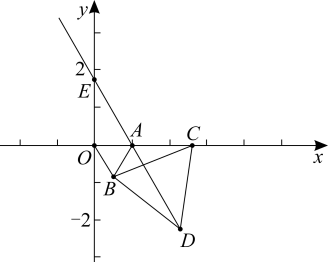
如图，在平面直角坐标系中，点A的坐标为（1，0），以线段OA为边在第四象限内作等边三角形△AOB，点C为x轴正半轴上一动点（），连接BC，以线段BC为边在第四象限内作等边三角形△CBD，连接DA并延长，交y轴于点E．

1. 如图，在平面直角坐标系中，点A的坐标为（1，0），以线段OA为边在第四象限内作等边三角形△AOB，点C为x轴正半轴上一动点（ $\text{[math]}$ ），连接BC，以线段BC为边在第四象限内作等边三角形△CBD，连接DA并延长，交y轴于点E．

(1) 求证：△OBC≌△ABD．

(2) 在点C的运动过程中，∠CAD的度数是否会变化？如果不变，请求出∠CAD的度数；如果变化，请说明理由．

(3) 以A，E，C为顶点的三角形是等腰三角形时，直接写出此时点C的坐标和CD的长度．

【考点】

坐标与图形性质; 等腰三角形的判定; 等边三角形的性质; 勾股定理; 三角形全等的判定-SAS;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 在菱形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 是射线 $\text{[math]}$ 上一动点，以 $\text{[math]}$ 为边向右侧作等边三角形 $\text{[math]}$ ，点 $\text{[math]}$ 的位置随点 $\text{[math]}$ 位置的变化而变化，连接 $\text{[math]}$ ．

(1) 如图①，当点 $\text{[math]}$ 在菱形 $\text{[math]}$ 内部或边上时，求证： $\text{[math]}$ ；

(2) 如图②、图③，请分别写出线段 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 之间的数量关系，不需证明．

综合题普通

2. 已知：点P(2m+4，m-1).试分别根据下列条件，求出P点的坐标.

(1) 点P在y轴上；

(2) 点P的纵坐标比横坐标大3；

(3) 点P在过A(2，-4)点且与x轴平行的直线上.

综合题普通

3. 在平面直角坐标系xOy中，对于点P（x，y），若点Q的坐标为（ax+y，x+ay），其中a为常数，则称点Q是点P的“a级关联点”．例如，点P（1，4）的“3级关联点”为Q（3×1+4，1+3×4），即Q（7，13）．

(1) 已知点A（﹣2，6）的“ $\text{[math]}$ 级关联点”是点A₁ ，点B的“2级关联点”是B₁（3，3），求点A₁和点B的坐标；

(2) 已知点M（m﹣1，2m）的“﹣3级关联点”M′位于y轴上，求M′的坐标；

(3) 已知点C（﹣1，3），D（4，3），点N（x，y）和它的“n级关联点”N′都位于线段CD上，请直接写出n的取值范围．

综合题普通