1.
定义:若两个三角形中,有两组边对应相等且其中一组等边所对的角对应相等,但不是全等三角形,我们就称这两个三角形为偏等三角形.

(1)
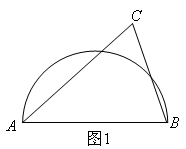
如图1,点C是 的中点,∠DAB是
的中点,∠DAB是 所对的圆周角,AD>AB,连结AC、DC、CB,试说明△ACB与△ACD是偏等三角形.
(2)
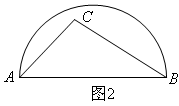
如图2,△ABC与△DEF是偏等三角形,其中∠A=∠D,AC=DF,BC=EF,则∠B+∠E=.请填写结论,并说明理由.
(3)
如图3,△ABC内接于⊙O,AC=4,∠A=30°,∠B=105°,若点D在⊙O上,且△ADC与△ABC是偏等三角形,AD>CD,求AD的值.
所对的圆周角,AD>AB,连结AC、DC、CB,试说明△ACB与△ACD是偏等三角形.
(2)
如图2,△ABC与△DEF是偏等三角形,其中∠A=∠D,AC=DF,BC=EF,则∠B+∠E=.请填写结论,并说明理由.
(3)
如图3,△ABC内接于⊙O,AC=4,∠A=30°,∠B=105°,若点D在⊙O上,且△ADC与△ABC是偏等三角形,AD>CD,求AD的值.
【考点】
圆周角定理;
圆内接四边形的性质;
三角形的外接圆与外心;
解直角三角形;
三角形全等的判定-SAS;