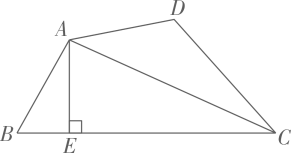
定义：一组对角互补，且对角线平分其中一个内角，称四边形为余缺四边形. 如图1，四边形，，平分，则四边形为余缺四边形.

1. 定义：一组对角互补，且对角线平分其中一个内角，称四边形为余缺四边形.

如图1，四边形 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 平分 $\text{[math]}$ ，则四边形 $\text{[math]}$ 为余缺四边形.

(1) 【概念理解】
用（填序号）一定可以拼成余缺四边形.

①两个全等的直角三角形， ②两个全等的等边三角形；

(2) 如图1，余缺四边形 $\text{[math]}$ ， $\text{[math]}$ 平分 $\text{[math]}$ ，若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ ；

(3)

【初步应用】

如图2，已知△ABC，∠BAC的平分线AP与BC的垂直平分线交于P点，连接PB、PC.

求证：四边形ABPC为余缺四边形；

(4) 若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的值为.

(5) 【迁移应用】
如图3， $\text{[math]}$ ，等腰 $\text{[math]}$ 的B、C两点分别在射线 $\text{[math]}$ 上，且斜边 $\text{[math]}$ (P、A在 $\text{[math]}$ 两侧)，若B、C两点在射线 $\text{[math]}$ 、 $\text{[math]}$ 上滑动时，四边形 $\text{[math]}$ 的面积是否发生变化？若不变化，请说明理由；若变化，直接写出面积的最大的值.

【考点】

三角形的面积; 直角三角形全等的判定-HL; 角平分线的性质; 勾股定理; 定义新运算;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 已知：如图，D为△ABC外角∠ACP平分线上一点，且DA=DB，DM⊥BP于点M.

(1) 若AC=6，DM=2，求△ACD的面积；

(2) 求证：AC=BM+CM.

综合题普通

2. 等面积法是一种常用的、重要的数学解题方法.

(1) 如图1，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的长为：.

(2) 如图2，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的高 $\text{[math]}$ 与 $\text{[math]}$ 的比是： .

(3) 如图3，在 $\text{[math]}$ 中， $\text{[math]}$ ，点D，P分别在边 $\text{[math]}$ ， $\text{[math]}$ 上，且 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，垂足分别为点E，F.若 $\text{[math]}$ ，求 $\text{[math]}$ 的值.

综合题普通

3. 如图，在四边形ABCD中，AB=AD，BC>CD，AC平分∠BCD，过点A作AE⊥BC，垂足为点E．

(1) 求证：CE=CD+BE；

(2) 如果CE=3BE，求 $\text{[math]}$ 的值．

综合题普通