1.
如图,正三角形、正方形、正六边形等正n边形与圆的形状有差异,我们将正n边形与圆的接近程度称为“接近度”.
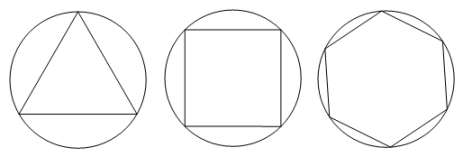
(1)
角的“接近度”定义:设正n边形的每个内角的度数为 , 将正n边形的“接近度”定义为
, 将正n边形的“接近度”定义为 .于是
.于是 越小,该正n边形就越接近于圆,
(2)
边的“接近度”定义:设一个正n边形的外接圆的半径为R,正n边形的中心到各边的距离为d,将正n边形的“接近度”定义为
越小,该正n边形就越接近于圆,
(2)
边的“接近度”定义:设一个正n边形的外接圆的半径为R,正n边形的中心到各边的距离为d,将正n边形的“接近度”定义为 .分别计算
.分别计算 时边的“接近度”,并猜测当边的“接近度”等于多少时,正n边形就成了圆?
时边的“接近度”,并猜测当边的“接近度”等于多少时,正n边形就成了圆?
①若 , 则该正n边形的“接近度”等于.
②若 , 则该正n边形的“接近度”等于.
③当“接近度”等于.时,正n边形就成了圆.
【考点】
三角形的外接圆与外心;
圆内接正多边形;
锐角三角函数的定义;
定义新运算;
能力提升

