如图，⊙O的直径AB的长为2，点C在圆周上，∠CAB=30°．点D是圆上一动点，DE∥AB交CA的延长线于点E，连接CD，交AB于点F．

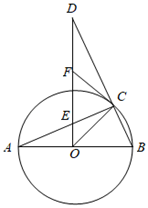
1. 如图，⊙O的直径AB的长为2，点C在圆周上，∠CAB=30°．点D是圆上一动点，DE∥AB交CA的延长线于点E，连接CD，交AB于点F．

(1) 如图1，当DE与⊙O相切时，求∠CFB的度数；

(2) 如图2，当点F是CD的中点时，求△CDE的面积．

【考点】

三角形的面积; 切线的性质; 圆的综合题;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 如图，AB是⊙O的直径，C是⊙O上一点，过点O作OD⊥AB，交BC的延长线于D，交AC于点E，F是DE的中点，连接CF．

(1) 求证：CF是⊙O的切线．

(2) 若∠A＝22.5°，求证：AC＝DC．

综合题普通

2. 如图1，E点为x轴正半轴上一点， $\text{[math]}$ 交x轴于A、B两点，交y轴于C、D两点，P点为劣弧 $\text{[math]}$ 上一个动点，且 $\text{[math]}$ 、 $\text{[math]}$ ．

(1) $\text{[math]}$ 的度数为 $\text{[math]}$ ；

(2) 如图2，连结 $\text{[math]}$ ，取 $\text{[math]}$ 中点G，连结 $\text{[math]}$ ，则 $\text{[math]}$ 的最大值为；

(3) 如图3，连接 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ ．若 $\text{[math]}$ 平分 $\text{[math]}$ 交 $\text{[math]}$ 于Q点，求 $\text{[math]}$ 的长；

(4) 如图4，连接 $\text{[math]}$ 、 $\text{[math]}$ ，当P点运动时（不与B、C两点重合），求证： $\text{[math]}$ 为定值，并求出这个定值．

综合题困难

3. 如图，AB是⊙O的直径，AB＝10，点D是半圆上的动点，点C是 $\text{[math]}$ 中点，

AC ， BD交于点E ，连接AD ．

(1) 如图1，若∠ABD＝30°，

①则∠CAD的度数为 ▲ ；

②求点E到AB的距离．

(2) 如图2，连接EO ，将EO绕点E顺时针旋转90°，点O的对应点F恰好落在AD上，求证：OB＝EB ．

(3) 在（2）的条件下，连接BC并延长，交AD的延长线于点G ，求出四边形CEDG的面积．

综合题困难