在△ABC中，AB＝AC，∠BAC＝90°，AD是△ABC的角平分线．

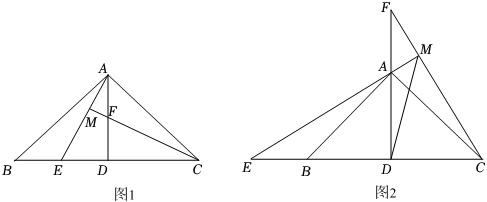
1. 在△ABC中，AB＝AC，∠BAC＝90°，AD是△ABC的角平分线．

(1) 如图1，点E、F分别是线段BD、AD上的点，且DE＝DF，AE与CF的延长线交于点M，则AE与CF的数量关系是，位置关系是；

(2) 如图2，点E、F分别在DB和DA的延长线上，且DE＝DF，EA的延长线交CF于点M．

①（1）中的结论还成立吗？如果成立，请给出证明；如果不成立，请说明理由；

②连接DM，求∠EMD的度数；

③若DM＝6 $\text{[math]}$ ， ED＝12，求EM的长．

【考点】

三角形全等的判定; 三角形的综合;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

(1) 问题：如图①，在 $\text{[math]}$ 中， $\text{[math]}$ ， D为 $\text{[math]}$ 边上一点（不与点B，C重合），将线段 $\text{[math]}$ 绕点A逆时针旋转 $\text{[math]}$ 得到 $\text{[math]}$ ，连接 $\text{[math]}$ ，则线段 $\text{[math]}$ 和线段 $\text{[math]}$ 的数量关系是，位置关系是；

(2) 探索：如图②，在 $\text{[math]}$ 与 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，将 $\text{[math]}$ 绕点A旋转，使点D落在 $\text{[math]}$ 边上，试探索线段 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 之间满足的等量关系，并证明结论；

(3) 应用：如图3，在四边形 $\text{[math]}$ 中， $\text{[math]}$ ．若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的长．

综合题普通

2. 如图， $\text{[math]}$ ．

(1) 写出 $\text{[math]}$ 与 $\text{[math]}$ 的数量关系．

(2) 延长 $\text{[math]}$ 到点 $\text{[math]}$ ，使 $\text{[math]}$ ，延长 $\text{[math]}$ 到点 $\text{[math]}$ ，使 $\text{[math]}$ ，连结 $\text{[math]}$ ．求证： $\text{[math]}$ ．

(3) 在(2)的条件下，作 $\text{[math]}$ 的平分线，交 $\text{[math]}$ 于点 $\text{[math]}$ ，求证： $\text{[math]}$ ．

综合题普通

3. 在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ 的角平分线， $\text{[math]}$ 于点 $\text{[math]}$ ．

(1) 如图1，连接 $\text{[math]}$ ，求证： $\text{[math]}$ 是等边三角形；

(2) 点 $\text{[math]}$ 是线段 $\text{[math]}$ 上的一点（不与点 $\text{[math]}$ ， $\text{[math]}$ 重合），以 $\text{[math]}$ 为一边，在 $\text{[math]}$ 的下方作 $\text{[math]}$ ， $\text{[math]}$ 交 $\text{[math]}$ 延长线于点 $\text{[math]}$ ．请你在图2中画出完整图形，并直接写出 $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ 之间的数量关系；

(3) 如图3，点 $\text{[math]}$ 是线段 $\text{[math]}$ 上的一点，以 $\text{[math]}$ 为一边，在 $\text{[math]}$ 的下方作 $\text{[math]}$ ， $\text{[math]}$ 交 $\text{[math]}$ 延长线于点 $\text{[math]}$ ．试探究 $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ 数量之间的关系，并说明理由．

综合题困难