1.
综合与实践
问题情境:数学课上,同学们以等腰直角三角形为背景,探究线段之间的数量关系.
已知:在Rt△ABC中,AC=BC,∠ACB=90°,D是射线CB上的一个动点,连接AD,过点C作AD的垂线,垂足为点E,过点B作AC的平行线交CE的延长线于点F.
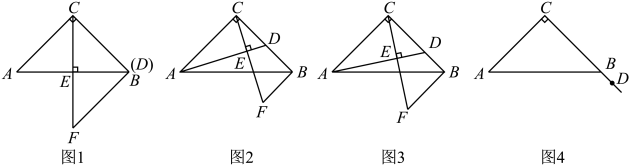
独立思考:
(1)
如图1,当点D与点B重合时,小颖发现BF=AC,请你帮她说明理由;
(2)
如图2,当点D为BC中点时,直接写出线段BF与AC的数量关系;
(3)
①如图3,当点D在线段CB上(不与C、B重合),请探究线段BF、BD与AC之间的数量关系(要求:写出发现的结论,并说明理由).
合作交流:
②如图4,当点D在线段CB延长线上,请探究线段BF、BD与AC之间的数量关系(要求:画出图形,写出发现的结论,并说明理由).
【考点】
平行线的性质;
三角形内角和定理;
等腰三角形的性质;
线段的中点;
三角形全等的判定-ASA;
能力提升



