如图，BD是矩形ABCD的对角线.

1. 如图，BD是矩形ABCD的对角线.

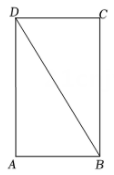
(1) 求作⊙A，使得⊙A与BD相切（要求：尺规作图，不写作法，保留作图痕迹）；

(2) 在（1）的条件下，设BD与⊙A相切于点E，CF⊥BD，垂足为F.若直线CF与⊙A相切于点G，求 $\text{[math]}$ 的值.

【考点】

正方形的判定与性质; 切线的性质; 锐角三角函数的定义; 尺规作图-垂线; 三角形全等的判定-AAS;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 菱形ABCD中，两条对角线AC，BD相交于点O，∠MON+∠BCD=180°，∠MON绕点O旋转，射线OM交边BC于点E，射线ON交边DC于点F，连接EF．

(1) 如图1，当∠ABC=90°时，△OEF的形状是；

(2) 如图2，当∠ABC=60°时，请判断△OEF的形状，并说明理由；

(3) 在（1）的条件下，将∠MON的顶点移到AO的中点O′处，∠MO′N绕点O′旋转，仍满足∠MO′N+∠BCD=180°，射线O′M交直线BC于点E，射线O′N交直线CD于点F，当BC=4，且 $\text{[math]}$ = $\text{[math]}$ 时，直接写出线段CE的长．

综合题困难

如图（1），在Rt△ABC，∠ACB=90°，分别以AB、BC为一边向外作正方形ABFG、BCED，连结AD、CF，AD与CF交于点M．

(1) 求证：△ABD≌△FBC；

(2) 如图（2），已知AD=6，求四边形AFDC的面积；

(3) 在△ABC中，设BC=a，AC=b，AB=c，当∠ACB≠90°时，c²≠a²+b² ．在任意△ABC中，c²=a²+b²+k．就a=3，b=2的情形，探究k的取值范围（只需写出你得到的结论即可）．

综合题普通