1.
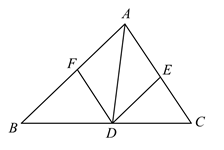
菱形ABCD中，两条对角线AC，BD相交于点O，∠MON+∠BCD=180°，∠MON绕点O旋转，射线OM交边BC于点E，射线ON交边DC于点F，连接EF．
(1)
如图1，当∠ABC=90°时，△OEF的形状是；
(2)
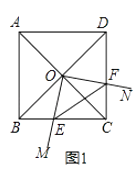
如图2，当∠ABC=60°时，请判断△OEF的形状，并说明理由；
(3)
在（1）的条件下，将∠MON的顶点移到AO的中点O′处，∠MO′N绕点O′旋转，仍满足∠MO′N+∠BCD=180°，射线O′M交直线BC于点E，射线O′N交直线CD于点F，当BC=4，且 
= 
时，直接写出线段CE的长．
【考点】
正方形的判定与性质;
