1.
《几何原本》是古希腊数学家欧几里得的一部不朽著作,是数学发展史的一个里程碑.在该书的第2幕“几何与代数”部分,记载了很多利用几何图形来论证的代数结论,利用几何给人以强烈印象将抽象的逻辑规律体现在具体的图形之中.
(1)
我们在学习许多代数公式时,可以用几何图形来推理,观察下列图形,找出可以推出的代数公式,(下面各图形均满足推导各公式的条件,只需填写对应公式的序号)
(2)
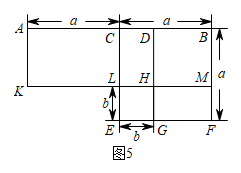
《几何原本》中记载了一种利用几何图形证明平方差公式 的方法,如图5,请写出证明过程;(已知图中各四边形均为矩形)
(3)
如图6,在等腰直角三角形ABC中,
的方法,如图5,请写出证明过程;(已知图中各四边形均为矩形)
(3)
如图6,在等腰直角三角形ABC中, , D为BC的中点,E为边AC上任意一点(不与端点重合),过点E作
, D为BC的中点,E为边AC上任意一点(不与端点重合),过点E作 于点G,作
于点G,作 F点H过点B作BF//AC交EG的延长线于点F.记△BFG与△CEG的面积之和为
F点H过点B作BF//AC交EG的延长线于点F.记△BFG与△CEG的面积之和为 , △ABD与△AEH的面积之和为
, △ABD与△AEH的面积之和为 .
.
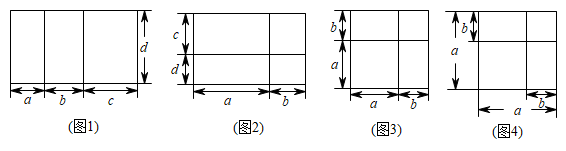
公式①:
公式②:
公式③:
公式④:
图1对应公式,图2对应公式,图3对应公式,图4对应公式;
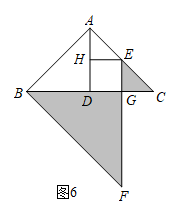
①若E为边AC的中点,则的值为 ▲ ;
②若E不为边AC的中点时,试问①中的结论是否仍成立?若成立,写出证明过程;若不成立,请说明理由.
【考点】
多项式乘多项式;
三角形的面积;
正方形的性质;
等腰直角三角形;
能力提升


