1.
如图，在△ABC中，D是BC边上的点（不与点B、C重合），连结AD．
问题引入：
(1)
如图①，当点D是BC边上的中点时，S△ABD：S△ABC=；当点D是BC边上任意一点时，S△ABD：S△ABC=（用图中已有线段表示）．
(2)
如图②，在△ABC中，O点是线段AD上一点（不与点A、D重合），连结BO、CO，试猜想S△BOC与S△ABC之比应该等于图中哪两条线段之比，并说明理由．
(3)
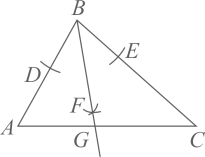
如图③，O是线段AD上一点（不与点A、D重合），连结BO并延长交AC于点F，连结CO并延长交AB于点E，试猜想 
+ 
+ 
的值，并说明理由．
【考点】
三角形的面积;
能力提升
真题演练
