1.
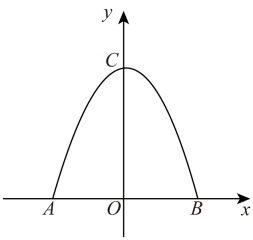
如图是一块铁皮余料,将其放置在平面直角坐标系中,底部边缘 在
在 轴上,且
轴上,且 dm,外轮廓线是抛物线的一部分,对称轴为
dm,外轮廓线是抛物线的一部分,对称轴为 轴,高度
轴,高度 dm.现计划将此余料进行切割:
dm.现计划将此余料进行切割:
(1)
若切割成正方形,要求一边在底部边缘 上且面积最大,求此正方形的面积;
(2)
若切割成矩形,要求一边在底部边缘
上且面积最大,求此正方形的面积;
(2)
若切割成矩形,要求一边在底部边缘 上且周长最大,求此矩形的周长;
(3)
若切割成圆,判断能否切得半径为
上且周长最大,求此矩形的周长;
(3)
若切割成圆,判断能否切得半径为 dm的圆,请说明理由.
dm的圆,请说明理由.
【考点】
二次函数的最值;
待定系数法求二次函数解析式;
矩形的性质;
切线的性质;
二次函数图象上点的坐标特征;
能力提升
