0 返回首页
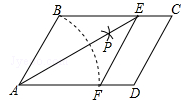
1. 如图，在菱形ABCD中，对角线AC、BD相交于点O，点E是AD的中点，连接OE，过点D作DF∥AC交OE的延长线于点F，连接AF.

(1) 求证：△AOE≌△DFE；
(2) 判定四边形AODF的形状并说明理由.
【考点】
平行线的性质; 菱形的性质; 矩形的判定; 三角形全等的判定-ASA;
【答案】

您现在未登录，无法查看试题答案与解析。 登录
综合题 普通
能力提升
换一批
1. 已知线段a＝4cm．

(1) 用尺规作图作一个边长为4cm的菱形ABCD，使∠A＝60°（保留作图痕迹），
(2) 求这个菱形的面积．
综合题 普通
2. 如图所示，五边形ABCDE是张大爷十年前承包的一块土地的示意图．经过多年开垦荒地，现已变成如图所示的形状，但承包土地与开垦荒地的分界小路（即图中折线CDE）还保留着，张大爷想过E点修一条直路，直路修好后，要保持直路左边的土地面积与承包时的一样多，右边的土地面积与开垦的荒地面积一样多．请你用有关的几何知识，按张大爷的要求设计出修路方案．（不计分界小路与直路的占地面积）

(1) 写出设计方案，并在图中画出相应的图形；
(2) 说明方案设计理由．
综合题 普通
3. 如图，在▱ABCD中，以点A为圆心，AB长为半径画弧交AD于点F，再分别以点B、F为圆心，大于 BF的相同长为半径画弧，两弧交于点P；连接AP并延长交BC于点E，连接EF，则所得四边形ABEF是菱形．

(1) 根据以上尺规作图的过程，求证：四边形ABEF是菱形；
(2) 若菱形ABEF的周长为16，AE=4 ，求∠C的大小．
综合题 普通