0 返回首页
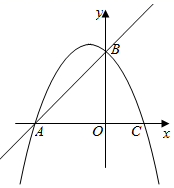
1. 在平面直角坐标系xOy中，抛物线y＝x2﹣2bx ．
(1) 当抛物线过点（2，0）时，求抛物线的表达式；
(2) 求这个二次函数的对称轴（用含b的式子表示）；
(3) 若抛物线上存在两点A（b﹣1，y1）和B（b+2，y2），当y1•y2＜0时，求b的取值范围．
【考点】
待定系数法求二次函数解析式; 二次函数与不等式（组）的综合应用;
【答案】

您现在未登录，无法查看试题答案与解析。 登录
综合题 普通
能力提升
真题演练
换一批
1. 对于抛物线y=ax2-4x+3(a>0)
(1) 若抛物线过点(4，3)

①求顶点坐标；

②当0≤x≤6时，直接写出y的取值范围为             ；
(2) 已知当0≤x≤m时，1≤y≤9，求a和m的值．
综合题 普通
2. 如图，在平面直角坐标系中，抛物线与x轴交于 ， ， 与y轴交于C点．

(1) 求抛物线的解析式；
(2) 若直线与抛物线交于 ， ， 请直接写出不等式的解集．
综合题 普通
3. 已知二次函数中的x和y满足下表：

x

⋯

-4

-3

-2

-1

0

1

2

⋯

y

⋯

-5

0

3

4

3

m

-5

⋯

(1) 根据表格，直接写出该二次函数的对称轴以及m的值；
(2) 求该二次函数的表达式．
综合题 普通