1.
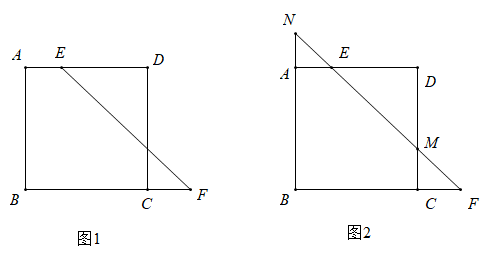
如图1,正方形 中,
中, 为对角线,点P在线段
为对角线,点P在线段 上运动,以
上运动,以 为边向右作正方形
为边向右作正方形 , 连接
, 连接 ;
;



(1)
则 与
与 的数量关系是,
的数量关系是, 与
与 的夹角度数为;
(2)
点P在线段
的夹角度数为;
(2)
点P在线段 及其延长线上运动时,探究线段
及其延长线上运动时,探究线段 ,
,  和
和 三者之间的数量关系,并说明理由;
(3)
当点P在对角线
三者之间的数量关系,并说明理由;
(3)
当点P在对角线 的延长线上时,连接
的延长线上时,连接 , 若
, 若 , 求四边形
, 求四边形 的面积.
的面积.
【考点】
正方形的性质;
等腰直角三角形;
几何图形的面积计算-割补法;
三角形全等的判定-SAS;