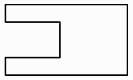
1.
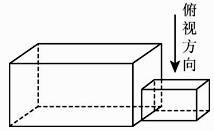
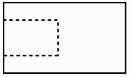
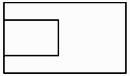
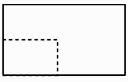
在一个正方体中,经过它的三个顶点的平面将该正方体截去一个三棱锥.所得多面体的三视图中,以图①为正视图,在图②③④⑤中选两个分别作为侧视图和俯视图,组成这个多面体的三视图,则所选侧视图和俯视图的编号依次为(写出符合要求的一组答案即可).

【考点】
空间几何体的三视图;
基础巩固
能力提升
变式训练
拓展培优
真题演练



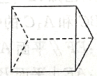









 图1
图1  图2
图2