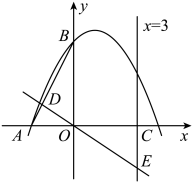
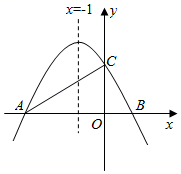
如图，在平面直角坐标系中，一次函数y=kx+2的图像与y轴交点为B，且与正比例函数的图像交于点C(m，4)．

1. 如图，在平面直角坐标系中，一次函数y=kx+2的图像与y轴交点为B，且与正比例函数 $\text{[math]}$ 的图像交于点C(m，4)．

(1) 求m的值及一次函数y=kx+2的表达式．

(2) 若点P是y轴上一点，且△BPC的面积为6，求点P的坐标．

【考点】

两一次函数图象相交或平行问题; 三角形的面积;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 如图，已知点A（3，0），C（﹣1，0），点B为y轴正半轴上的一点，且S_△ABC＝6.

(1) 求直线AB的解析式；

(2) 在y轴上是否存在点T，将直线CB沿直线CT翻折后，点B的对称点H恰好落在x轴上.若存在，求出T点的坐标；若不存在，说明理由.

(3) 若P、Q两点在直线AB上，且x_P、x_Q是方程x²﹣x﹣2mx+m²+m﹣2＝0的两个根，当∠POQ＝90°时，求m的值.

综合题困难

2. 如图，在平面直角坐标系中，过点B（6，0）的直线AB与直线OA相交于点A（4，2），与y轴相交于点C，动点M在线段OA和射线AC上运动．

(1) 求直线AB的解析式；

(2) 若△OMC的面积是△OAC的面积的 $\text{[math]}$ ，请直接写出此时点M的坐标．

综合题困难

3. 在平面直角坐标系xOy中，直线a：y=2x﹣6，和直线b：y=﹣ $\text{[math]}$ x+4相交于点H，分别与x、y轴交于点A、B、C、D，点P在x轴上，过点P作x轴的垂线，分别与直线a、b交于点E、F．

(1) 求点H的坐标；

(2) 判断直线a、b的位置关系，并说明理由；

(3) 设点P的横坐标为m，当m为何值时，以D、E、F、O为顶点的四边形是

平行四边形，说明理由．

综合题困难