如图，点A和点E(2，1)是反比例函数y＝（x＞0）图象上的两点，点B在反比例函数y＝（x＜0）的图象上，分别过点A，B作y轴的垂线，垂足分别为点C，D，AC＝BD，连接AB交y轴于点F.

1. 如图，点A和点E(2，1)是反比例函数y＝ $\text{[math]}$ （x＞0）图象上的两点，点B在反比例函数y＝ $\text{[math]}$ （x＜0）的图象上，分别过点A，B作y轴的垂线，垂足分别为点C，D，AC＝BD，连接AB交y轴于点F.

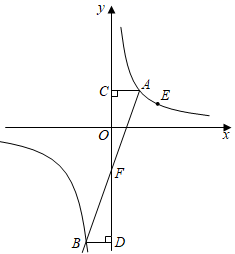
(1) k＝；

(2) 设点A的横坐标为a，点F的纵坐标为m，求证：am＝﹣2；

(3) 连接CE，DE，当∠CED＝90°时，直接写出点A的坐标：.

【考点】

待定系数法求反比例函数解析式; 三角形的面积; 勾股定理; 三角形全等的判定-AAS;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 设函数 $\text{[math]}$ ，函数 $\text{[math]}$ （ $\text{[math]}$ ， $\text{[math]}$ ， b是常数， $\text{[math]}$ ， $\text{[math]}$ ）．若函数 $\text{[math]}$ 和函数 $\text{[math]}$ 的图象交于点 $\text{[math]}$ ，点 $\text{[math]}$ ．

(1) 求点 $\text{[math]}$ ， $\text{[math]}$ 的坐标．

(2) 求函数 $\text{[math]}$ ， $\text{[math]}$ 的表达式．

(3) 当 $\text{[math]}$ 时，直接写出 $\text{[math]}$ 的取值范围．

综合题普通

2. 如图，一次函数 $\text{[math]}$ 的图象与 $\text{[math]}$ 轴、 $\text{[math]}$ 轴分别相交于 $\text{[math]}$ 、 $\text{[math]}$ 两点，与反比例函数 $\text{[math]}$ 的图象相交于点 $\text{[math]}$ ．

(1) 求反比例函数的表达式；

(2) 点 $\text{[math]}$ 的横坐标为4，过点 $\text{[math]}$ 作 $\text{[math]}$ 轴平行线，交反比例函数的图象于点 $\text{[math]}$ ，连接 $\text{[math]}$ 求 $\text{[math]}$ 的面积．

综合题普通

3. 如图，在平面直角坐标系 $\text{[math]}$ 中， $\text{[math]}$ 的边 $\text{[math]}$ 在x轴正半轴上， $\text{[math]}$ ， $\text{[math]}$ ， C为斜边 $\text{[math]}$ 的中点，反比例函数 $\text{[math]}$ 在第一象限内的图像经过点C，交边 $\text{[math]}$ 于点D．

(1) 这个反比例函数的解析式；

(2) 连结 $\text{[math]}$ ，求 $\text{[math]}$ 的值．

综合题普通