《淮南子･天文训》中记载了一种确定东西方向的方法，大意是：日出时，在地面上点处立一根杆，在地面上沿着杆的影子的方向取一点，使两点间的距离为10步（步是古代的一种长度单位），在点处立一根杆；日落时，在地面上沿着点处的杆的影子的方向取一点，使两点间的距离为10步，在点处立一根杆．取的中点，那么直线表示的方向为东西方向．

1. 《淮南子･天文训》中记载了一种确定东西方向的方法，大意是：日出时，在地面上点 $\text{[math]}$ 处立一根杆，在地面上沿着杆的影子的方向取一点 $\text{[math]}$ ，使 $\text{[math]}$ 两点间的距离为10步（步是古代的一种长度单位），在点 $\text{[math]}$ 处立一根杆；日落时，在地面上沿着点 $\text{[math]}$ 处的杆的影子的方向取一点 $\text{[math]}$ ，使 $\text{[math]}$ 两点间的距离为10步，在点 $\text{[math]}$ 处立一根杆．取 $\text{[math]}$ 的中点 $\text{[math]}$ ，那么直线 $\text{[math]}$ 表示的方向为东西方向．

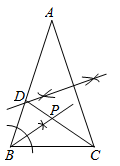
(1) 上述方法中，杆在地面上的影子所在直线及点 $\text{[math]}$ 的位置如图所示．使用直尺和圆规，在图中作 $\text{[math]}$ 的中点 $\text{[math]}$ （保留作图痕迹）；

(2) 在如图中，确定了直线 $\text{[math]}$ 表示的方向为东西方向．根据南北方向与东西方向互相垂直，可以判断直线 $\text{[math]}$ 表示的方向为南北方向，完成如下证明．

证明：在 $\text{[math]}$ 中， $\text{[math]}$ ▲ ， $\text{[math]}$ 是 $\text{[math]}$ 的中点，

$\text{[math]}$ ▲ （填推理的依据）．

∵直线 $\text{[math]}$ 表示的方向为东西方向，

∴直线 $\text{[math]}$ 表示的方向为南北方向．

【考点】

等腰三角形的性质; 尺规作图-垂直平分线;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 将一根长为 $\text{[math]}$ 的铁丝，剪掉一部分后，剩下部分围成一个等腰三角形（接头部分忽略不计），这个等腰三角形的底为 $\text{[math]}$ ，腰为 $\text{[math]}$ ．

(1) 求剪掉部分的铁丝长度．

(2) 若围成的等腰三角形的周长为 $\text{[math]}$ ，求铁丝的长度．

综合题普通

2. 下面是小石设计的“过直线上一点作这条直线的垂线”的尺规作图过程．

已知：如图1，直线l及直线l上一点P ．

求作：直线PQ ，使得PQ⊥l ．

作法：如图2：

①以点P为圆心，任意长为半径作弧，交直线l于点A ， B；

②分别以点A ， B为圆心，以大于 $\text{[math]}$ AB的同样长为半径作弧，两弧在直线l上方交于点Q；

③作直线PQ ．

所以直线PQ就是所求作的直线．

根据小石设计的尺规作图过程：

(1) 使用直尺和圆规，补全图形（保留作图痕迹）；

(2) 完成下面的证明．

证明：连接QA ， QB ．

∵QA＝ ▲ ， PA＝ ▲ ，

∴PQ⊥l （ ▲ ）（填推理的依据）．

综合题普通

3. 数学课上，张老师举了下面的例题：

例1 等腰三角形 $\text{[math]}$ 中， $\text{[math]}$ ，求 $\text{[math]}$ 的度数.（答案： $\text{[math]}$ ）

例2 等腰三角形 $\text{[math]}$ 中， $\text{[math]}$ ，求 $\text{[math]}$ 的度数.（答案： $\text{[math]}$ 或 $\text{[math]}$ 或 $\text{[math]}$ ）

张老师启发同学们进行变式，小敏编了如下一题：

变式等腰三角形 $\text{[math]}$ 中， $\text{[math]}$ ，求 $\text{[math]}$ 的度数.

(1) 请你解答以上的变式题.

(2) 解（1）后，小敏发现， $\text{[math]}$ 的度数不同，得到 $\text{[math]}$ 的度数的个数也可能不同.如果在等腰三角形 $\text{[math]}$ 中，设 $\text{[math]}$ ，当 $\text{[math]}$ 有三个不同的度数时，请你探索 $\text{[math]}$ 的取值范围.

综合题普通