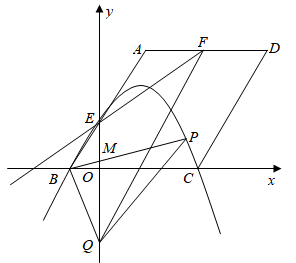
如图，在平面直角坐标系中，平行四边形的边与y轴交于E点，F是的中点，B、C、D的坐标分别为 .

1. 如图，在平面直角坐标系 $\text{[math]}$ 中，平行四边形 $\text{[math]}$ 的 $\text{[math]}$ 边与y轴交于E点，F是 $\text{[math]}$ 的中点，B、C、D的坐标分别为 $\text{[math]}$ .

(1) 求过B、E、C三点的抛物线的解析式；

(2) 试判断抛物线的顶点是否在直线 $\text{[math]}$ 上；

(3) 设过F与 $\text{[math]}$ 平行的直线交y轴于Q，M是线段 $\text{[math]}$ 之间的动点，射线 $\text{[math]}$ 与抛物线交于另一点P，当 $\text{[math]}$ 的面积最大时，求P的坐标.

【考点】

二次函数的最值; 待定系数法求二次函数解析式; 二次函数与一次函数的综合应用; 二次函数的实际应用-几何问题;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 在平面直角坐标系中，二次函数y＝ax²+bx+2的图象与x轴交于A（﹣3，0），B（1，0）两点，与y轴交于点C ．

(1) 求这个抛物线的函数解析式；

(2) 求直线AC的函数解析式；

(3) 点P是直线AC上方的抛物线上一动点，是否存在点P ，使△ACP的面积最大？若存在，求出点P的坐标；若不存在，说明理由．

综合题普通

2. 已知：抛物线 $\text{[math]}$ ： $\text{[math]}$ .

(1) 若顶点坐标为 $\text{[math]}$ ，求b和c的值（用含a的代数式表示）；

(2) 当 $\text{[math]}$ 时，求函数 $\text{[math]}$ 的最大值；

(3) 若不论m为任何实数，直线 $\text{[math]}$ 与抛物线 $\text{[math]}$ 有且只有一个公共点，求a ， b ， c的值；此时，若 $\text{[math]}$ 时，抛物线的最小值为k ，求k的值.

综合题困难

3. 如图，已知抛物线 $\text{[math]}$ 与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ， $\text{[math]}$ ，与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ，与直线 $\text{[math]}$ 交于 $\text{[math]}$ ， $\text{[math]}$ 两点．

(1) 求该抛物线的函数表达式；

(2) 若在第一象限的抛物线上有一点 $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ ，求四边形 $\text{[math]}$ 面积的最大值；

(3) 抛物线上是否存在一点 $\text{[math]}$ ，使得 $\text{[math]}$ ？若存在，请求出点 $\text{[math]}$ 的坐标；若不存在，请说明理由．

综合题困难