1.
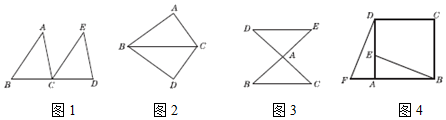
如图,  由
由  绕点
绕点  按逆时针方向旋转
按逆时针方向旋转  得到,且点B的对应点D恰好落在BC的延长线上,AD,EC相交于点P.
得到,且点B的对应点D恰好落在BC的延长线上,AD,EC相交于点P.

(1)
求∠BDE的度数;
(2)
 是
是  延长线上的点,且∠CDF=∠DAC.判断DF和PF的数量关系,并证明.
延长线上的点,且∠CDF=∠DAC.判断DF和PF的数量关系,并证明.
【考点】
旋转的性质;
旋转对称图形;
能力提升
真题演练