1.
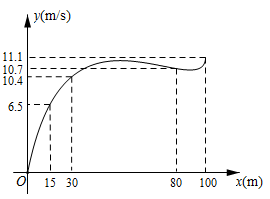
根据数学家凯勒的“百米赛跑数学模型”,前30米称为“加速期”,30米~80米为“中途期”,80米~100米为“冲刺期”.市田径队把运动员小斌某次百米跑训练时速度y(m/s)与路程x(m)之间的观测数据,绘制成曲线如图所示.
(1)
y是关于x的函数吗?为什么?
(2)
“加速期”结束时,小斌的速度为多少?
(3)
根据如图提供的信息,给小斌提一条训练建议.
【考点】
函数的概念;
通过函数图象获取信息;
能力提升
真题演练



