1.
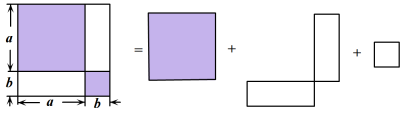
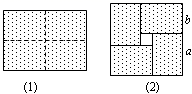
将一个长为  ,宽为
,宽为  的矩形纸片
的矩形纸片  ,用剪刀沿图1中的虚线剪开,分成四块形状和大小都一样的小矩形纸片,然后按图2的方式拼成一个正方形,则中间小正方形的面积为( )
,用剪刀沿图1中的虚线剪开,分成四块形状和大小都一样的小矩形纸片,然后按图2的方式拼成一个正方形,则中间小正方形的面积为( )

A.
 B.
B.
 C.
C.
 D.
D.

【考点】
完全平方公式的几何背景;