0 返回首页
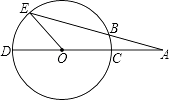
1. 如图，在Rt△ABC中，∠BAC=90°，以点A为圆心，AC长为半径作圆，交BC于点D，交AB于点E，连结DE.

(1) 若∠ABC=20°，求∠DEA的度数；
(2) 若AC=3，AB=4，求CD的长.
【考点】
等腰三角形的性质; 勾股定理; 圆的相关概念;
【答案】

您现在未登录，无法查看试题答案与解析。 登录
综合题 普通
能力提升
真题演练
换一批
1. 如图所示，在Rt△ABC中，∠B=90°，AB=6cm，CB=3cm，点P在AC上以cm/s的速度从点A匀速运动至点C停止，点Q沿BA方向以2cm/s的速度运动，当点P不与点A重合时，连结PQ，以PQ、BQ为邻边作平行四边形PQBM，当P点停止运动时，点Q也随之停止运动，设点P的运动时间为t(s)．

(1) AC=
(2) 当四边形PQBM为矩形时，求t的值；
(3) 当△PQM是钝角三角形时，求t的取值范围．
综合题 普通
2. 如图，CD是⊙O的直径，点A在DC的延长线上，∠A=20°，AE交⊙O于点B，且AB=OC．

(1) 求∠AOB的度数．
(2) 求∠EOD的度数．
综合题 普通
3. 如图，在每个小正方形的边长均为1的方格纸中，有线段AB，点A、B均在小正方形的顶点上．

(1) 在方格纸中画出以AB为一边的直角△ABC，点C在小正方形的顶点上，且△ABC的面积为3．
(2) 在方格纸中将△ABC绕点C逆时针旋转90°，画出旋转后△DEC（点A与点D对应，点B与点E对应），请直接写出点A绕着点C旋转的路径长．
综合题 普通