抛物线y＝x2﹣2ax﹣a﹣3与x轴交于点A，B，与y轴交于点C，点D（4，﹣a﹣3）在抛物线的图象上.

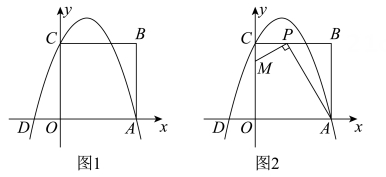
1. 抛物线y＝x²﹣2ax﹣a﹣3与x轴交于点A，B，与y轴交于点C，点D（4，﹣a﹣3）在抛物线的图象上.

(1) 求抛物线的解析式；

(2) 现规定平面直角坐标系中横纵坐标相等的点为“不动点”.已知点N（x_N ， y_N），Q（x_Q ， y_Q）是抛物线y＝x²﹣2ax﹣a﹣3图象上的“不动点”，点H是点N，Q之间抛物线上一点（不与点N，Q重合），求点H的纵坐标的取值范围.

【考点】

二次函数的最值;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 已知函数 $\text{[math]}$ 为常数）的图象经过点 $\text{[math]}$ ．

(1) 求 $\text{[math]}$ 满足的关系式；

(2) 设该函数图象的顶点坐标是 $\text{[math]}$ ，当 $\text{[math]}$ 的值变化时，求 $\text{[math]}$ 关于 $\text{[math]}$ 的函数解析式；

(3) 设该函数的图象不经过第三象限，当-5 $\text{[math]}$ 时，函数的最大值与最小值之差为16，求 $\text{[math]}$ 的值．

综合题普通

2. 已知函数y=-x²+bx+c（b，c为常数）的图象经过点（0，﹣3），（﹣6，﹣3）．

(1) 求b，c的值．

(2) 当﹣4≤x≤0时，求y的最大值．

(3) 当m≤x≤0时，若y的最大值与最小值之和为2，求m的值．

综合题普通

3. 已知二次函数 $\text{[math]}$ ，其中 $\text{[math]}$ .

(1) 当 $\text{[math]}$ 时，求二次函数顶点坐标；

(2) 当 $\text{[math]}$ 时，记二次函数的最小值为 $\text{[math]}$ ，求证： $\text{[math]}$ ；

(3) 当 $\text{[math]}$ 时，且 $\text{[math]}$ 满足 $\text{[math]}$ 时，函数有最大值为3，求 $\text{[math]}$ 的值.

综合题困难