1.
实验探究:
(1)
动手操作:
(2)
猜想证明:
(3)
灵活应用:
(4)
如图5,∠ABD,∠ACD的10等分线相交于点F1、F2、…、F9 ,
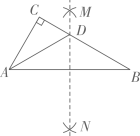
①如图1,将一块直角三角板DEF放置在直角三角板ABC上,使三角板DEF的两条直角边DE、DF分别经过点B、C,且BC∥EF,已知∠A=30°,则∠ABD+∠ACD=;

②如图2,若直角三角板ABC不动,改变等腰直角三角板DEF的位置,使三角板DEF的两条直角边DE、DF仍然分别经过点B、C,那么∠ABD+∠ACD=;

如图3,∠BDC与∠A、∠B、∠C之间存在着什么关系,并说明理由;

请你直接利用以上结论,解决以下列问题:
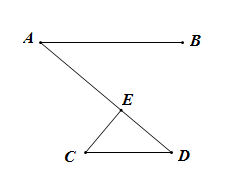
如图4,BE平分∠ABD,CE平分∠ACD,若∠BAC=40°,∠BDC=120°,求∠BEC的度数;

若∠BDC=120°,∠BF3C=64°,则∠A的度数为.

【考点】
三角形内角和定理;