1.
如图1和2,在正方形  中,点
中,点  、
、  在经过点
在经过点  的直线
的直线  上,
上,  为等腰直角三角形,
为等腰直角三角形,  ,且点
,且点  始终在
始终在  的内部,连结
的内部,连结  .
.

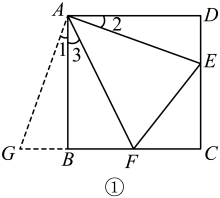
(1)
当直线  绕点
绕点  旋转到如图1所示的位置时,求证:①
旋转到如图1所示的位置时,求证:①  ;②
;②  ;③
;③  ;
(2)
当直线
;
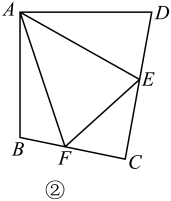
(2)
当直线  绕点
绕点  旋转到如图2所示的位置时,探究:(1)中的①、②、③三个结论是否仍然成立?若不成立,请直接写出正确的结论(不必证明);
(3)
在直线
旋转到如图2所示的位置时,探究:(1)中的①、②、③三个结论是否仍然成立?若不成立,请直接写出正确的结论(不必证明);
(3)
在直线  绕点
绕点  旋转过程中,若正方形
旋转过程中,若正方形  的边长为
的边长为  ,
,  ,求
,求  的长.
的长.
【考点】
三角形全等的判定;
勾股定理;
正方形的性质;
锐角三角函数的定义;
等腰直角三角形;
能力提升