如图，在△ABC中，AE为∠BAC的角平分线，点D为BC的中点，DE⊥BC交AE于点E，EG⊥AC于点G．

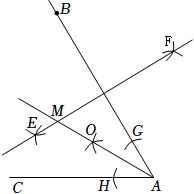
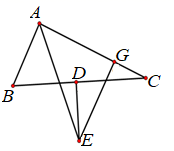
1. 如图，在△ABC中，AE为∠BAC的角平分线，点D为BC的中点，DE⊥BC交AE于点E，EG⊥AC于点G．

(1) 求证： AB+AC=2AG．

(2) 若BC=8cm，AG=5cm，求△ABC的周长．

【考点】

角平分线的性质; 线段垂直平分线的性质;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

综合题普通

综合题普通

已知：如图1，线段a和线段b．

求作： $\text{[math]}$ ，使得 $\text{[math]}$ ， $\text{[math]}$ ， BC边上的中线为b．

作法：如图2，

①作射线BM，并在射线BM上截取 $\text{[math]}$ ；

②作线段BC的垂直平分线PQ，PQ交BC于点D；

③以点D为圆心，b为半径作弧，交PQ于点A；

④连接AB和AC．

则 $\text{[math]}$ 为所求作的等腰三角形．

证明：由作图可知 $\text{[math]}$ ， $\text{[math]}$ ．

∵PQ为线段BC的垂直平分线，点A在PQ上，

∴ $\text{[math]}$ （ ▲ ）（填推理的依据）．

又∵线段BC的垂直平分线PQ交BC于点D，

∴ $\text{[math]}$ ．

∴AD为BC边上的中线．

综合题普通