如图，抛物线y= x2+bx+c与x轴交于A、B两点，与y轴交于点C，其对称轴交抛物线于点D，交x轴于点E，已知OB=OC=6．

1.

如图，抛物线y= $\text{[math]}$ x²+bx+c与x轴交于A、B两点，与y轴交于点C，其对称轴交抛物线于点D，交x轴于点E，已知OB=OC=6．

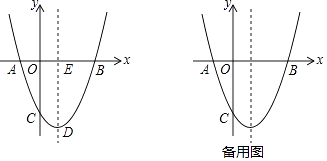
(1) 求抛物线的解析式及点D的坐标；

(2) 连接BD，F为抛物线上一动点，当∠FAB=∠EDB时，求点F的坐标；

(3) 平行于x轴的直线交抛物线于M、N两点，以线段MN为对角线作菱形MPNQ，当点P在x轴上，且PQ= $\text{[math]}$ MN时，求菱形对角线MN的长．

【考点】

二次函数图象与坐标轴的交点问题; 菱形的性质; 相似三角形的性质; 相似三角形的判定与性质; 二次函数y=ax²+bx+c与二次函数y=a（x-h）²+k的转化;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 如图，抛物线 $\text{[math]}$ 与x轴交于点 $\text{[math]}$ ， $\text{[math]}$ ，与y轴交于点C．

(1) 求抛物线对应的函数解析式，并直接写出顶点P的坐标；

(2) 求 $\text{[math]}$ 的面积．

注：抛物线 $\text{[math]}$ 的对称轴是直线 $\text{[math]}$ ，顶点坐标是 $\text{[math]}$ ．

综合题普通

2. 如图，已知一次函数 $\text{[math]}$ 的图象分别与 $\text{[math]}$ 轴 $\text{[math]}$ 轴交于点 $\text{[math]}$ ， $\text{[math]}$ ，在二次函数 $\text{[math]}$ 中， $\text{[math]}$ 是一个不为0的常数.

(1) 若二次函数的图象过点 $\text{[math]}$ ，则 $\text{[math]}$ 的值是；

(2) 点 $\text{[math]}$ 是二次函数图象的顶点，连接 $\text{[math]}$ ，若 $\text{[math]}$ ，求 $\text{[math]}$ 的值；

(3) 二次函数的图象与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ，与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ，设点 $\text{[math]}$ 的横坐标为 $\text{[math]}$ ，且 $\text{[math]}$ ，连接 $\text{[math]}$ .能使 $\text{[math]}$ 与坐标轴所成的夹角等于 $\text{[math]}$ 的 $\text{[math]}$ 有几个？请直接写出 $\text{[math]}$ 的值.

综合题普通

3. 在平面直角坐标系xOy中，已知抛物线y=x²﹣4x+2m﹣1与x轴交于点A，B.（点A在点B的左侧）

(1) 求m的取值范围；

(2) 当m取最大整数时，求点A、点B的坐标.

综合题普通