如图，长方形AOBC，以O为坐标原点，OB、OA分别在x轴、y轴上，点A的坐标为（0，8），点B的坐标为（10，0），点E是BC边上一点，把长方形AOBC沿AE翻折后，C点恰好落在x轴上点F处．

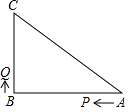
1. 如图，长方形AOBC，以O为坐标原点，OB、OA分别在x轴、y轴上，点A的坐标为（0，8），点B的坐标为（10，0），点E是BC边上一点，把长方形AOBC沿AE翻折后，C点恰好落在x轴上点F处．

(1) 求点E、F的坐标；

(2) 求AF所在直线的函数关系式；

(3) 在x轴上求一点P，使△PAF成为以AF为腰的等腰三角形，请直接写出所有符合条件的点P的坐标．

【考点】

坐标与图形性质; 等腰三角形的判定; 勾股定理; 矩形的性质; 翻折变换（折叠问题）;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 如图，已知△ABC中，∠B=90°，AB=8cm，BC=6cm，P、Q是△ABC边上的两个动点，其中点P从点A开始沿A→B方向运动，且速度为每秒1cm，点Q从点B开始沿B→C方向运动，且速度为每秒2cm，它们同时出发，设出发的时间为t秒．

(1) 当t=2秒时，求PQ的长；

(2) 求出发时间为几秒时，△PQB是等腰三角形？

(3) 若Q沿B→C→A方向运动，则当点Q在边CA上运动时，求能使△BCQ成为等腰三角形的运动时间．

综合题普通

2. 我们新定义一类三角形：有两边的平方和等于第三边平方的2倍的三角形叫做奇异三角形．例如，某三角形的三边长分别是2， $\text{[math]}$ ，因为 $\text{[math]}$ =2 $\text{[math]}$ ，所以这个三角形是奇异三角形

(1) 若△ABC的三边长分别是3，4和 $\text{[math]}$ ，判断此三角形是否为奇异三角形，请说明理由．

(2) 若Rt△ABC是奇异三角形，直角边分别为a，b，斜边为c，请探究a和b满足的数量关系式．

综合题普通

3. 某校八年（1）班的小华和小轩学习了“勾股定理”之后，为了测得风筝的垂直高度 $\text{[math]}$ ，他们进行了如下操作：

①测得水平距离 $\text{[math]}$ 的长为12米：

②根据手中剩余线的长度计算出风筝线 $\text{[math]}$ 的长为20米：

③牵线放风筝的小明的身高为1.5米．

(1) 求风筝的垂直高度 $\text{[math]}$ ：

(2) 如果小明想风筝沿 $\text{[math]}$ 方向再下降4米，则他应该再收回多少米线？

综合题普通